Les intérêts composés fonctionnent selon un mécanisme où les intérêts générés par un capital initial sont réinvestis, augmentant ainsi la base de calcul des intérêts pour les périodes suivantes.
Contrairement aux intérêts simples, qui ne sont calculés que sur le capital de départ, les intérêts composés permettent de faire fructifier à la fois le capital initial et les intérêts déjà accumulés. Ce processus crée un effet boule de neige, car chaque période, les intérêts ajoutés au capital produisent eux-mêmes de nouveaux intérêts.
Le réinvestissement des intérêts est l’un des deux éléments clés du fonctionnement des intérêts composés, l’autre étant le temps, qui joue un rôle crucial dans l’intensification de cet effet exponentiel.
Par exemple, un placement de 1000 € à 5 % par an donne 50 € d’intérêts la première année, portant le capital à 1050 € ; la deuxième année, les intérêts sont calculés sur 1050 €, générant 52,50 €, et ainsi de suite.
Ce fonctionnement est utilisé dans divers produits financiers, comme les comptes d’épargne (par exemple, le livret A) ou les placements à long terme, et permet une croissance significative du capital sur le long terme.
Comment calculer les intérêts cumulés ?
Pour calculer les intérêts composés, vous pouvez utiliser la formule suivante :
Cn = Co(1+i)^n
- Cn est le capital final après n périodes,
- Co est le capital initial,
- i est le taux d’intérêt par période,
- n est le nombre de périodes.
Pour bien visualiser l’accumulation des intérêts, il peut être intéressant de construire un tableau de capitalisation. Par exemple, si vous voulez suivre l’évolution d’un placement sur 5 ans avec un taux d’intérêt annuel de 4%, vous pouvez organiser votre tableau de cette manière :
| Année | Capital de départ | Intérêts de l’année | Capital de fin d’année |
|---|---|---|---|
| 1 | Co | Co*i | Co*(1+i) |
| 2 | Co*(1+i) | Co*(1+i)*i | Co*(1+i)^2 |
| 3 | Co*(1+i)^2 | Co*(1+i)^2*i | Co*(1+i)^3 |
| 4 | Co*(1+i)^3 | Co*(1+i)^3*i | Co*(1+i)^4 |
| 5 | Co*(1+i)^4 | Co*(1+i)^4*i | Co*(1+i)^5 |
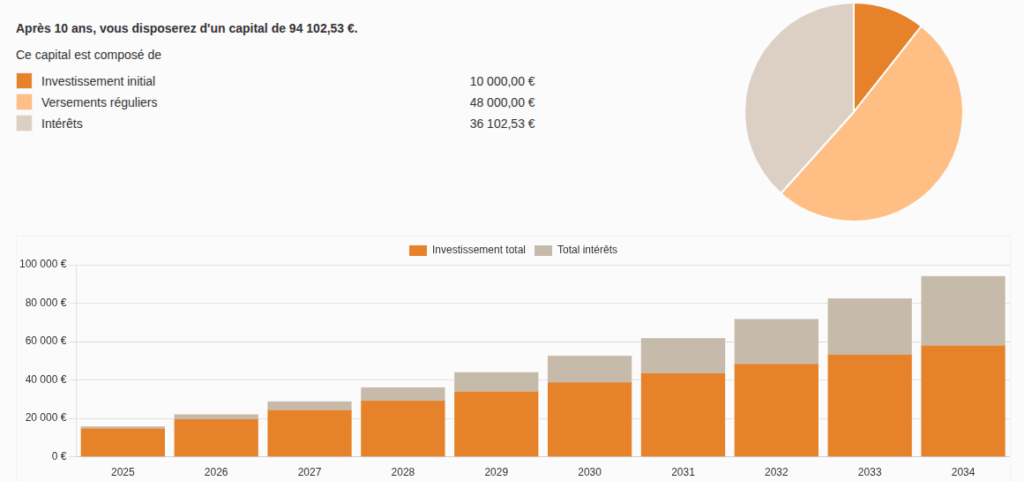
Exemple ci-dessous avec un investissement de départ de 10000 euros, puis 400€/mois avec un taux d’intérêt de 8% sur 10 ans :
| Année | Investissement | Intérêts | Solde |
|---|---|---|---|
| 2025 | 14 800,00 € | 1 005,55 € | 15 805,55 € |
| 2026 | 4800,00 € | 1 470,00 € | 22 075,55 € |
| 2027 | 4800,00 € | 1 971,61 € | 28 847,15 € |
| 2028 | 4800,00 € | 2 513,32 € | 36 160,48 € |
| 2029 | 4800,00 € | 3 098,39 € | 44 058,87 € |
| 2030 | 4800,00 € | 3 730,27 € | 52 589,14 € |
| 2031 | 4800,00 € | 4 412,69 € | 61 801,82 € |
| 2032 | 4800,00 € | 5 149,70 € | 71 751,52 € |
| 2033 | 4800,00 € | 5 945,69 € | 82 497,20 € |
| 2034 | 4800,00 € | 6 805,33 € | 94 102,53 € |
| Totaux | 58 000,00 € | 36 102,53 € | 94 102,53 € |
36 102,53 € d’intérêts sur 10 ans ! Pas mal, non ?
Les intérêts composés dans le domaine de l’investissement
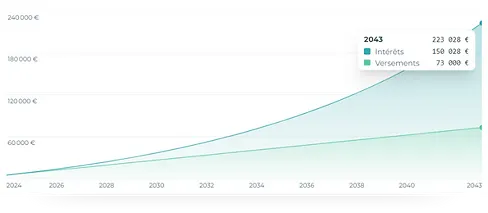
En investissement, les intérêts composés sont considérés comme un puissant levier de croissance. En effet, ils permettent d’augmenter la valeur de votre investissement de façon exponentielle, surtout sur le long terme.
Ils sont donc particulièrement intéressants pour les investisseurs ayant une stratégie d’investissement à long terme.
Les intérêts composés s’appliquent à divers types de placements : livrets d’épargne, assurance vie, PER, bourse…
Comment doubler son capital en 1 an grâce aux intérêts composés ?
Pour doubler son capital, une méthode couramment utilisée est la règle de 72. Il s’agit d’une d’une formule simple pour estimer le temps nécessaire pour doubler un investissement grâce aux intérêts composés.
Pour cela il suffit de diviser 72 par le taux d’intérêt annuel. Par exemple, si vous avez un taux d’intérêt de 6%, cela prendrait environ 12 ans (72/6) pour doubler votre capital. Un taux d’intérêt de 12% doublerait votre capital en 6 ans.
Cependant, pour atteindre cet objectif en un an, il faudrait un taux d’intérêt exceptionnellement élevé. En effet, selon la règle de 72, vous auriez besoin d’un taux d’intérêt mensuel de 6% pour doubler votre investissement en un an…
Comment investir dans les intérêts composés ? L’association des versements programmés
Pour tirer le meilleur parti des intérêts composés, l’association avec les versements programmés est une stratégie efficace. Cette méthode consiste à investir une somme fixe à des intervalles réguliers (mensuels, trimestriels, etc.), indépendamment des fluctuations du marché.
Cette technique, aussi appelée “dollar-cost averaging” (DCA), permet de réduire le risque lié à la volatilité des marchés en achetant plus d’actifs lorsque les prix sont bas et moins lorsque les prix sont élevés.
Avec les versements programmés, vos gains sont réinvestis, ce qui augmente votre capital de manière exponentielle grâce à l’effet des intérêts composés. Ainsi, votre capital initial et les versements réguliers profitent de l’effet de capitalisation sur le long terme.
Einstein considèrait les intérêts composés comme « la force la plus puissante de l’univers », « la meilleure invention de l’humanité » ou « la huitième merveille du monde »

Laisser un commentaire